
Exploring the Fourth Dimension
For centuries, geometry has described physical space using three spatial dimensions: length, width, and height. Modern mathematics, however, provides a consistent framework for spaces of higher dimension, where additional coordinates extend beyond ordinary spatial intuition.
Within this context, we introduce the Tetracron as a geometric and conceptual framework for interpreting four-dimensional domains through the accumulation of three-dimensional volumes. Rather than proposing a new physical dimension, this work offers an organized geometric perspective that makes higher-dimensional structure more accessible to spatial reasoning.


The Tetracron Principle: A Geometric Interpretation of the Fourth Dimension as a Foliation of Three-Dimensional Volumes
Author: Cesar A. Valencia Z.
Affiliation: Independent Researcher
Abstract
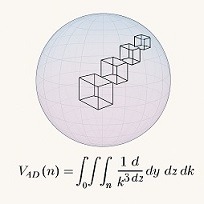
This work proposes the Tetracron Principle, an interpretative geometric framework for understanding the fourth spatial dimension. The approach is based on an idea consistent with the classical mathematical formulation of higher-dimensional spaces: a four-dimensional domain can be represented as a parameterized family of three-dimensional volumes. This description is related to the notion of foliation and to the iterated decomposition of multiple integrals, as formalized in well-established results of mathematical analysis (e.g., the Fubini–Tonelli theorem).
The contribution of the present work does not lie in the introduction of a new formal structure, but rather in a geometric and pedagogical reinterpretation that emphasizes the construction of 4D objects through the ordered accumulation of three-dimensional “layers.” This viewpoint facilitates the conceptual visualization of polytopes, hypervolumes, and growth processes in higher dimensions, serving as a bridge between mathematical formalism and spatial intuition.
Geometric examples, structural consequences of the approach, and potential lines of application in higher-dimensional geometry, mathematical modeling, and theoretical frameworks involving four-dimensional spaces are presented.
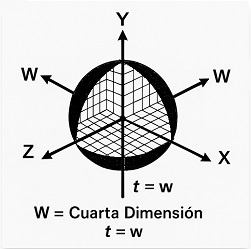
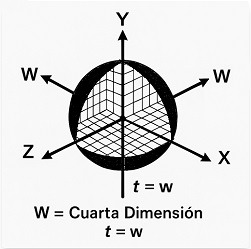
1. Introduction and Motivation
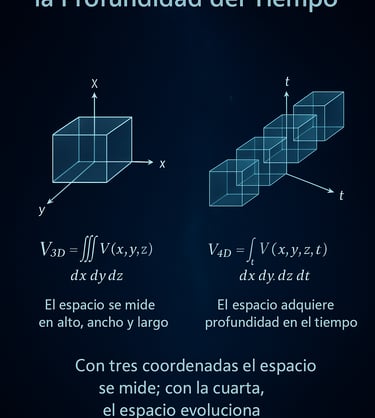
In three-dimensional geometry, volumes can be described as the continuous accumulation of areas, as occurs in the construction of solids of revolution or in the integral formulation of volume. This viewpoint, deeply connected to the development of calculus, provides a direct link between geometric intuition and analytical formalization.
By analogy, a four-dimensional domain can be represented as a parameterized family of three-dimensional volumes depending on a fourth coordinate. From a mathematical standpoint, this property is grounded in the theory of product measures and in the iterated decomposition of multiple integrals, as formalized in classical results of analysis.
The proposal of this work is to formulate this interpretation as an explicit conceptual framework — here termed the Tetracron Principle — with the aim of organizing and facilitating the geometric visualization of the fourth dimension. In this sense, the approach maintains a pedagogical affinity with Cavalieri’s historical idea of comparing volumes through sections, although its purpose is not to introduce a new mathematical structure, but rather to systematically highlight a geometric perspective already implicit in the existing formalism.
4. Formal Justification
The mathematical foundation of this interpretation lies in the theory of product measures and in the iterated decomposition of multiple integrals. In particular, if
7. Conclusion
The Tetracron Principle proposes a coherent and intuitive geometric framework for interpreting four-dimensional domains as parameterized families of three-dimensional volumes. Its foundation lies in classical results from measure theory and multiple integration, while its principal contribution resides in the conceptual and organizational formulation of this perspective.
Rather than extending the existing mathematical apparatus, the principle aspires to serve as a tool for visualization, pedagogical articulation, and support for geometric reasoning in contexts involving higher-dimensional spaces. In this sense, it acts as a bridge between analytical formalism and spatial intuition, encouraging interdisciplinary exploration while remaining within the established mathematical framework.
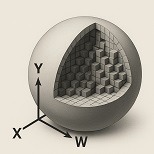
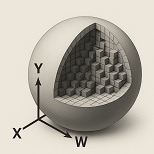


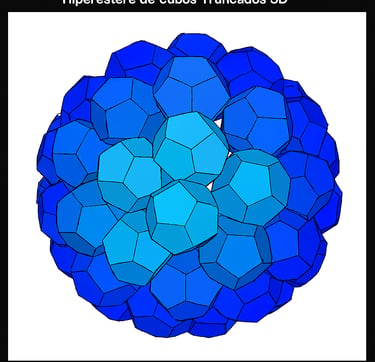
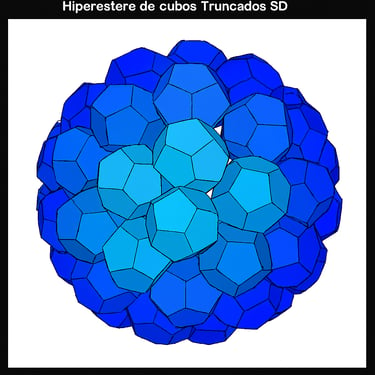


Hypersphere
Hypercube
4D Prisms
where
represents the three-dimensional section of the set along the coordinate w, and μ3 denotes the Lebesgue measure in
This result establishes that, under standard measurability conditions, a four-dimensional domain can be described as a parameterized family of three-dimensional volumes. The relevance of the Tetracron Principle does not lie in the technical novelty of this decomposition — which is well known in mathematical analysis — but in its geometric reading: a 4D object may be visualized as a continuous accumulation of 3D “layers,” in the same way that a 3D volume can be conceived as the accumulation of 2D areas.
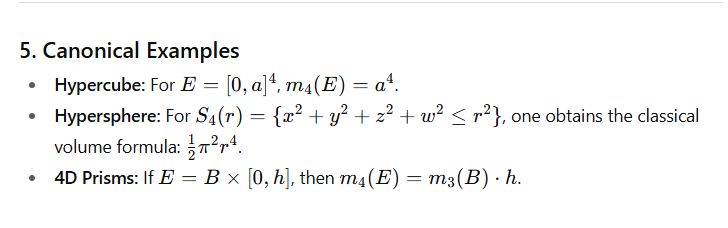
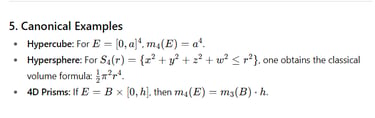
6. Discussion
The Tetracron Principle does not aim to introduce a new result in measure theory, but rather to propose an explicit interpretative framework for a geometric structure already implicit in the existing mathematical formalism.
By assigning a name and conceptual organization to this perspective, the principle provides a unifying way to approach the visualization of four-dimensional domains through parameterized three-dimensional sections. In this sense, it maintains a methodological affinity with historical approaches that used sections to understand higher-dimensional magnitudes, although its purpose is primarily structural and pedagogical.
This viewpoint may prove useful in contexts where geometric intuition plays a relevant role, such as higher-dimensional geometry, multiscale mathematical modeling, certain formulation schemes in mathematical physics, and the study of structured growth processes (for example, fractal or biological geometric models). These potential applications should be understood as conceptual avenues of exploration rather than as direct consequences of the principle.


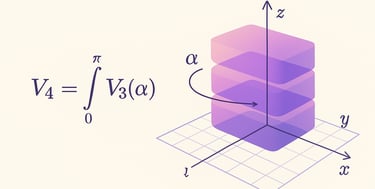

is a measurable set (in the Lebesgue sense), its measure can be expressed as an iterated integral with respect to one of its coordinates, according to the Fubini–Tonelli theorem:



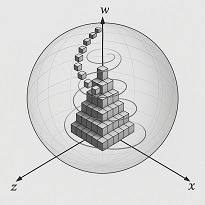
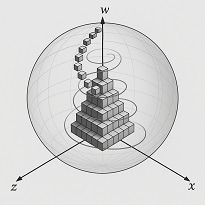


New dimension
Explore the geometry of the fourth dimension and discover a new understanding of time and space.
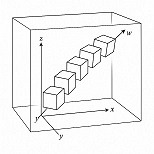
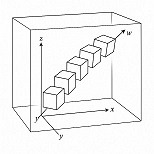

Space games
An interactive and playful approach to the mathematical concepts of the fourth dimension and their influence on perception.
Advanced mathematics
Explore the mathematical formulation of the Tetracron and its implications for our understanding of the universe.
Creative exploration
Learn and experience the geometry of the fourth dimension through different aspects of the world around us.
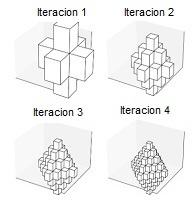
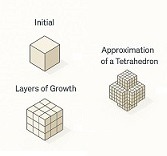
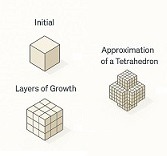
Cubic-Tetrahedric accumulation
Visualizes how the accumulation of a cube along an additional dimension generates a four-dimensional solid.
Hyperspheric accumulation
An accumulation governed by isotropic forces — equal in all directions — leads to the formation of a four-dimensional sphere.
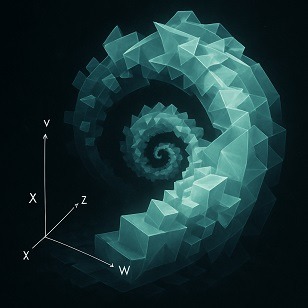
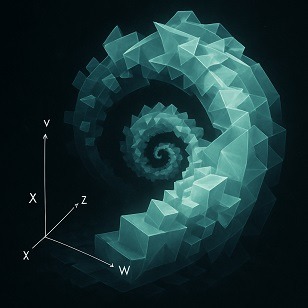
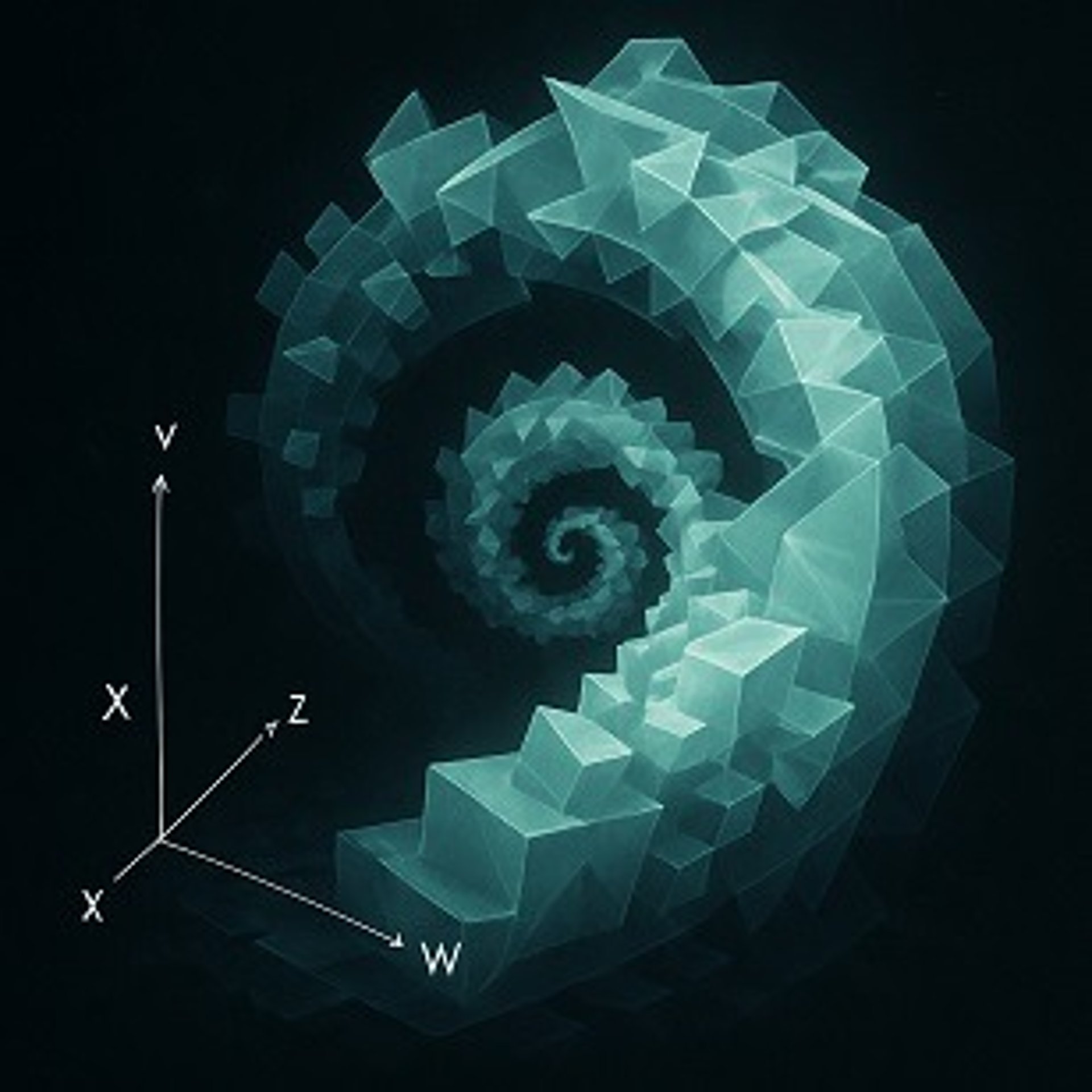
Helical accumulation
If a three-dimensional solid is asymmetric, its accumulation along an additional dimension, combined with the rotational displacement arising from successive accommodation, gives rise to a helical four-dimensional structure.
Tetrachron Gallery
Explore the geometry of the fourth dimension and its meaning.










Explore the geometry of the fourth dimension with us.


Dimensión
Exploreing geometry of fourth dimension.
Math
space
avcesar58@hotmail.com
© 2025. All rights reserved.