1. Why the Tetrachron Principle allows 4D solids to be emulated

The Tetrachron Principle defines a universal constructive rule for generating four-dimensional objects:

Every four-dimensional solid is obtained as the continuous accumulation of three-dimensional volumes along a fourth coordinate w.

This means that mathematicians and computational physicists no longer need to imagine 4D as an abstract entity —
they can simulate it as an integral sequence of 3D volumes.

Each Ew represents a 3D layer, and m4(E) gives its total four-dimensional measure.
This provides a computational and geometric framework to build and measure tetrachrons precisely.

2. Practical applications

Using this principle, a scientist or engineer can:

• Model a 4D solid via a function Ew​ describing the change of 3D shape along w.

• Visualize each layer in 3D software (Blender, MATLAB, Mathematica) and project the 4D body.

• Compute its total hypervolume directly through integration.

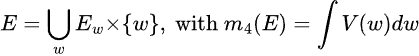
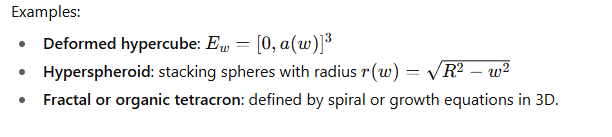
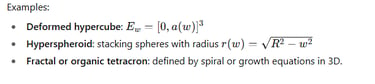
3. Why it’s revolutionary

Traditional 4D mathematics has remained abstract—rooted in analytical theorems (Fubini–Tonelli) or regular polytopes.
The Tetrachron Principle brings a physical and generative interpretation:

The fourth dimension is not a conceptual leap but a continuous process of spatial accumulation.

It allows anyone to:

• Construct tetracrons.

• Measure them exactly.

• Visualize them through 3D sections.

• Simulate their real-time growth.

4. What makes it new

The Fubini–Tonelli Theorem ensures the commutativity of integration.
The Tetrachron Principle transforms that analytical property into a law of spatial generation.

It doesn’t merely integrate — it creates space itself.

This conceptual leap defines the Tetrachron as a new foundation for four-dimensional geometry.